https://codeforces.com/contest/1237
https://codeforces.com/blog/entry/70620 (Editorial)
A B C1 C2 D E F G H의 9문제가 나왔는데, 나는 A B까지 푼 후 생각이 막혀서 1시간 반을 버리고 마지막에 C1 C2 D를 풀었다. 레이팅이 100 가까이 떨어져서 Grand master에서 International master가 되었다.
A. Balanced Rating Changes
길이가 $N$인 수열 $\{a_0, a_1, ..., a_{N-1}\}$이 주어진다. $\sum a_i=0$이다. $b_i=\lfloor \frac{a_i}{2} \rfloor$ or $b_i=\lceil \frac{a_i}{2} \rceil$, $\sum b_i=0$인 수열 $\{b_0, b_1, ..., b_{N-1}\}$을 구하여라.
$a_i$가 짝수라면 $b_i$는 $\frac{a_i}{2}$로 결정된다. 홀수인 $a_i$의 절반은 $b_i=\lfloor \frac{a_i}{2} \rfloor$로 하고, 나머지 절반은 $b_i=\lceil \frac{a_i}{2} \rceil$로 하면 된다. 따라서 $O(N)$에 풀 수 있다.
B. Balanced Tunnel
터널에 $N$개의 차가 차례대로 들어갔다. $i$번째로 들어간 차는 $A_i$이고, $i$번째로 나온 차는 $B_i$이다($i\neq j \leftrightarrow A_i \neq A_j$, $\{A_1, A_2, ..., A_N\} = \{B_1, B_2, ..., B_N\}$). 터널 안에서 한 번 이상 추월을 한 것으로 확신할 수 있는 차의 수는?
$A_i=B_j$일 경우 $C_i=j$로 놓자. 차 $x$가 추월을 했다는 것은, 터널에 들어갈 때는 $x$보다 앞에 있었으나 나올 때는 $x$보다 뒤에 있는 차가 있다는 것이다. 따라서 $A_i$가 추월을 했는지 알기 위해서는 $j<i$, $C_j > C_i$인 $j$가 있는지 확인하면 된다. 이것은 $mx_i=$max($C_j$|$j<i$)를 알면 된다. $mx_i>C_i$이면 추월을 한 것이다. 따라서 $O(N)$에 풀 수 있다.
나는 BIT를 이용해서 풀었다. 그러면 $O(NlogN)$이다.
C. Balanced Removals
좌표공간에 서로 다른 점 $N$개가 주어진다($N$은 짝수). $i$번 점의 좌표는 ($x_i, y_i, z_i$)이다. 두 점을 골라서 지우는 연산을 $\frac{N}{2}$번 반복할 것이다. 이때, 점 $a, b$를 고르기 위해서는 min($x_a, x_b$) $\leq x_c \leq$ max($x_a, x_b$) and min($y_a, y_b$) $\leq y_c \leq$ max($y_a, y_b$) and min($z_a, z_b$) $\leq z_c \leq$ max($z_a, z_b$)인 아직 지워지지 않은 점 $c$가 있으면 안된다. 점들을 어떠한 순서로 지워야할 지 구하여라.
점들을 $x$ 좌표 순으로 정렬한다. 이제 $x$ 좌표가 같은 점들끼리 짝을 지어 없애서, 특정 $x$ 좌표를 가지는 점을 1개 이하로 남길 것이다. 그러면 남은 점들은 $x$ 좌표 순으로 정렬한 뒤 두 개씩 짝을 지으면 된다. 이제 $x$ 좌표가 같은 점들을 없애는 과정을 생각하자. 이 점들을 $y$ 좌표 순으로 정렬한 후 $y$ 좌표 같은 점들을 1개 이하로만 남길 것이다. 그러면 남은 점들은 $y$ 좌표 순으로 정렬한 뒤 두 개씩 짝을 지으면 된다. 이제 $x, y$ 좌표가 같은 점들을 1개 이하로 남기는 과정을 생각하자. 이 점들은 한 직선상에 있고 $z$ 좌표가 모두 다르다. 따라서 $z$ 좌표 순으로 정렬한 뒤 두 개씩 짝지으면 된다. 이 과정을 거치면 $O(NlogN)$으로 풀 수 있다.
나는 이 문제를 잘못 읽었고, 그 사실을 안 것은 D를 푼 후였다.
D. Balanced Playlist
플레이리스트에 $N$개의 곡이 들어있다. 플레이리스트의 곡들은 차례대로 틀어지고, 마지막에 도달하면 다시 처음부터 시작한다. $i$번째 곡의 coolness는 $x_i$이다. 특정 곡부터 듣기 시작해서, 지금 나오는 노래의 coolness가 여태 나온 노래들의 coolness의 최댓값의 절반 미만이 되면 노래를 그만 듣는다. $i$번째 곡부터 듣기 시작할 경우 몇 곡을 듣게 될지를 $i=1, ..., N$에 대해 차례로 구해라. 만약 곡을 무한히 계속 듣게 된다면 $-1$을 출력하라.
$i$번째 곡부터 듣기 시작했을 때, 곡을 무한히 듣지 않는다고 하자. 그러면 $N$번 안에 coolness가 최대인 노래를 듣고, 그 다음 $N$번 안에 coolness가 최소인 노래를 듣게 된다. 따라서 $N$개의 곡을 반복적으로 듣는 것이 아니라, $3N$개의 노래를 반복 없이 듣는다고 생각할 수 있다. 이제 각 곡에서 시작할 경우 몇 곡을 듣게 되는지 구하자. $i$번째 곡부터 듣기 시작할 경우 $s_i$번째 곡에서 그만듣는다고 하자.
첫 번째 접근은 $i$가 큰 $s_i$부터 구하는 것이다. $j=$min{$l$ | $l > j, A_l > A_j$ }, $k=$min{$l$ | $l > j, A_l < \frac{A_j}{2}$}라 하자. $j<k$이면 $s_i=s_j$이다. $j>k$이면 $s_i=k$이다. 이러한 $j$ 또는 $k$가 없다면 $s_i=-1$이다. $j, k$를 구하는 것은 segment tree를 이용하면 된다. 구체적으로는, 각 노드가 수열 $A$의 특정 구간에서의 최댓값과 최솟값을 가지게 하면 된다. 그러면 $O(NlogN)$으로 해결할 수 있다. 나는 dynamic segment tree로 해결을 했다. 그러면 $O(NlogX)$에 해결할 수 있다. ($X$는 $A_i$의 범위이다.)
두 번째 접근은 $i<j \leftrightarrow s_i<s_j$임을 관찰하는 것이다. 그러면 two pointer 방식을 이용할 수 있다. $i=1$부터 차례대로 보고, $p=s_{i-1}$로 놓는다. $A_p$가 max($A_i, ..., A_p$)의 절반 미만이면 $s_i=p$이다. 그렇지 않으면 $p$를 1 늘린 후 반복하면 된다. max($A_i, ..., A_p$)를 구하기 위해서는 sliding window 방식을 이용한다. 그러면 최댓값을 $O(1)$로 구할 수 있어서 $O(N)$에 문제를 해결할 수 있다. 나는 이 방법이 첫 번째 접근보다 속도는 2배 이상 빠르고 코드는 3배 이상 짧았다.
E. Balanced Binary Search Tree
$N$개의 정점을 가지는 Perfectly Balanced striped Binary Search Tree를 만들 것이다. 이는 아래 세 조건을 만족하는 트리를 의미한다.
1. Perfectly Balanced : 각 정점의 깊이의 합이 최소여야 한다.
2. striped : 모든 정점에 대해, 왼쪽 자식이 있다면 자신과 왼쪽 자식의 기우성이 달라야 한다. 오른쪽 자식이 있다면 자신과 오른쪽 자식의 기우성이 같아야 한다.
3. Binary Search Tree : Binary Search Tree이어야 하고, 각 정점의 값은 1, ..., $N$ 중 하나여야 하며 서로 달라야 한다.
$N$이 주어졌을 때, Perfectly Balanced striped Binary Search Tree의 개수를 구하여라.
Perfectly Balanced striped Binary Search Tree를 줄여서 PBSBST라고 부르겠다. 깊이가 $d$인 PBSBST를 생각하자. 1번 조건은, 이 트리가 깊이 $d-1$까지는 포화 이진트리여야 한다는 것이다.(루트의 깊이를 1로 정의하겠다.) 3번 조건을 통해, 트리의 모양이 정해지면 정점에 수를 부여하는 방법은 유일하게 결정된다는 것을 알 수 있다. 따라서 가능한 트리의 형태를 살펴보자.
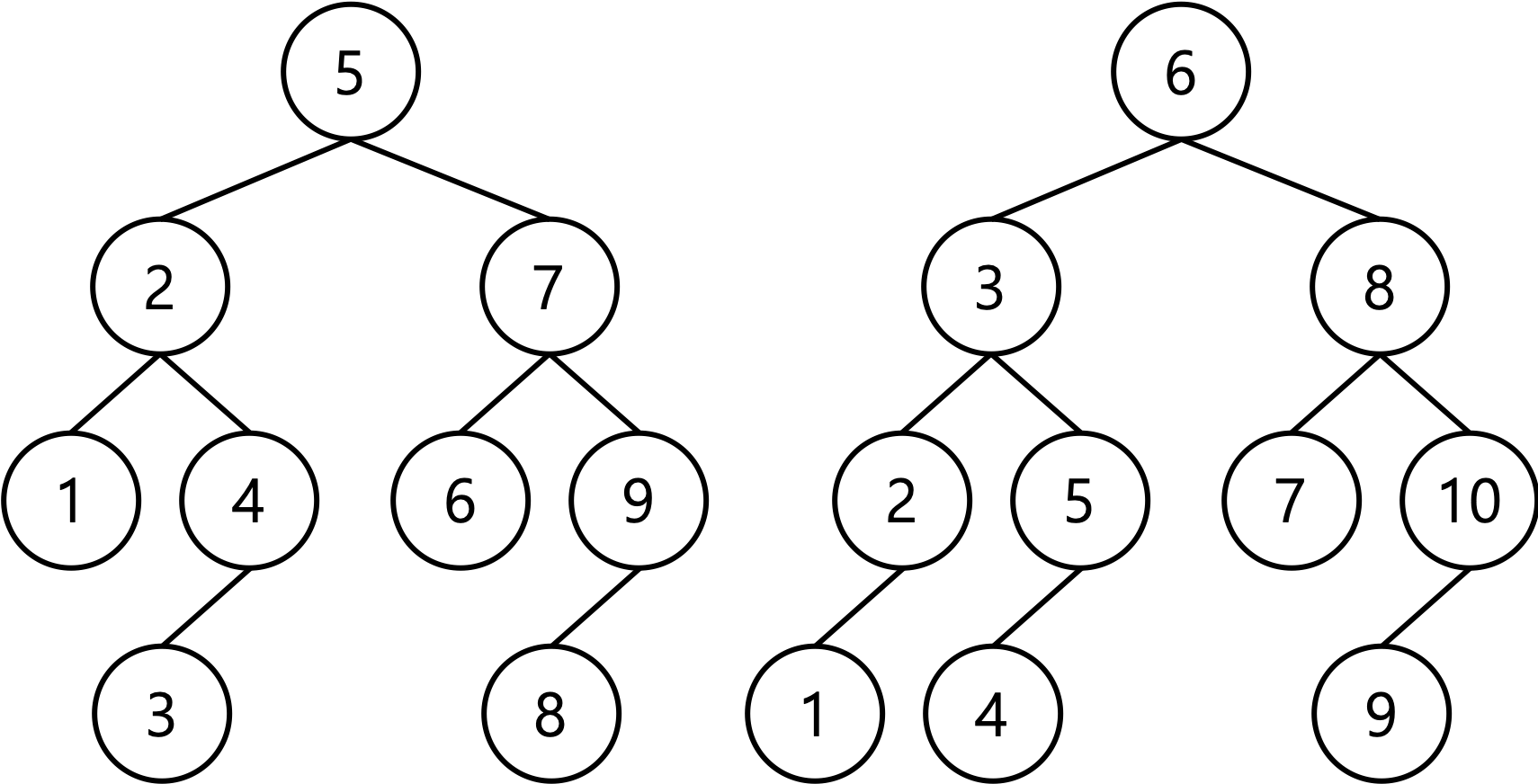
깊이가 $d$인 PBSBST는 2개 뿐이며, 이 두 가지 트리는 크기가 1 차이나며 1번 정점의 깊이가 각각 $d$와 $d-1$이라는 것을 보일 것이다($d \geq 4$). 이 트리의 루트는 왼쪽 자식과 오른쪽 자식을 갖는다($\because$Pefectly Balanced). 양쪽 서브트리는 1, 2, 3의 조건을 모두 만족한다. 따라서 양쪽 서브트리는 깊이가 $d-1$인 PBSBST이거나 깊이가 $d-2$인 포화이진트리이다. 그러나 깊이가 2 이상인 포화이진트리는 striped 조건을 만족하지 못한다. 따라서 양쪽 서브트리는 모두 PBSBST이다. 오른쪽 서브트리의 첫 번째 정점을 $v$라 하자. 루트와 $v$는 기우성이 다르다. 따라서 $v$의 깊이는 짝수여야 한다. 그러므로 오른쪽 서브트리의 형태는 유일하게 정해진다. 왼쪽 서브트리는 두 가지가 가능하다. 따라서 깊이가 $d$인 PBSBST는 2개이고, 이 두 트리의 크기는 1 차이나며, 1번 정점의 깊이는 $d$와 $d-1$이다.
답이 1인 $N$은 1, 2, 4, 5, 9, 10, ... 이다. 나머지 $N$에 대해서는 답이 0이다.

F. Balanced Domino Placement
$h\times w$ 크기의 격자판이 있다. 이 판에 $1\times 2$ 크기의 도미노를 놓을 것이다. 도미노는 회전할 수 있으며, 한 칸은 하나의 도미노로만 덮을 수 있다. 이 때, 각 행에서 도미노로 덮여진 칸들은 모두 같은 도미노에 의해 덮여있어야 한다. 열에 대해서도 마찬가지이다. 주어진 격자판에는 $N$개의 도미노가 조건을 만족하게끔 이미 놓여있다. 여기서 도미노를 더 놓는 경우, 가능한 판의 상태의 경우의 수는?
각 행에 대해, 도미노에 의해 덮인 칸이 있는지 여부를 확인한다. 열에 대해서도 반복한다. 어떤 행이 아직 한 칸도 덮이지 않았다면, 그 행이 아직 남아있다고 표현하자. 열에 대해서도 마찬가지로 정의하자. 추가적으로 놓이는 도미노는 남아있는 행과 열들에만 놓일 수 있다. 남아있는 행의 수를 $h'$, 남아있는 열의 수를 $w'$이라 하자. $d_h$개의 도미노를 가로 방향으로 놓고, $d_v$개의 도미노를 세로로 놓는다고 하자. 가로 방향 도미노는 남아있는 행 1개와, 남아있는 연속된 열 2개를 고르면 된다. 세로 방향 도미노는 남아있는 연속된 행 2개와 남아있는 열 1개를 고르면 된다. 따라서 남아있는 행 중에서, $d_v$개의 쌍(연속되어 있는 행 2개)과 $d_h$개의 행을 골라야 한다. $R=$(남아있는 행 중에서 $d_v$개의 쌍을 고르는 경우의 수)는 dp를 통해 $O(h)$에 구할 수 있다. 남아있는 열 중에서는 $d_h$개의 쌍(연속되어 있는 열 2개)과 $d_v$개의 열을 골라야 한다. $C=$(남아있는 열 중에서 $d_h$개의 쌍을 고르는 경우의 수) 역시 dp로 구할 수 있다. $d_h$개의 가로 도미노와 $d_v$개의 세로 도미노를 놓는 경우의 수는 $RC\binom{h'-2d_v}{d_h}\binom{w'-2d_h}{d_v}d_h!d_v!$이다. 따라서 문제를 $O(hw)$에 해결할 수 있다.
G. Balanced Distribution
$N$명의 사람들이 원형으로 서 있다. $i$번째 사람은 $A_i$개의 돌을 가지고 있다. 이 때, 모든 사람들이 같은 양의 돌을 가지고 싶다. 이를 위해 meeting 을 진행할 수 있다. $x$번 위치에서 meeting을 진행할 경우 $x, x+1, ..., x+K-1$(mod $N$)번 사람 모인다. meeting이 진행되는 동안, 그 meeting에 참여한 사람들끼리는 자유롭게 돌을 주고받을 수 있다. 모든 사람이 같은 양의 돌을 가지기 위해 필요한 최소 meeting의 수와, 각 meeting을 진행해야 하는 위치, 각 meeting이 끝난 후 meeting에 참여한 사람들의 돌의 양을 구하여라. ($\sum A_i$이 $N$의 배수임이 보장된다.)
$i$번 사람과 $i+1$번 사람 사이에 문 $i$가 있다고 생각하자. $x$번 위치에서 meeting을 진행할 경우 $x, x+1, ..., x+K-2$번 문이 열러서 그 사이로 돌을 주고받을 수 있는 것이다. 문 $i$를 넘어가는 돌의 개수를 $p_i$라고 하자. $p_i>0$이면 $i$번 사람이 $i+1$번 사람에게 $p_i$개의 돌을 준 것이고, $p_i<0$이면 $i+1$번 사람이 $i$번 사람에게 $-p_i$개의 돌을 준 것이다. $p_{i+1} - p_i$은 유일하게 결정된다. 따라서 우리는 $\{p_i\}$에 일정한 상수를 더한 $\{q_i\}$를 구할 수 있다.
$p_i \neq 0$일 경우 $i$번 문은 한 번 이상 열려야 한다. $p_i=0$일 경우 그 문은 열어도 되고 열지 않아도 된다. 열지 않을 문 $s$와 $e$가 있다고 하자. 이 때, $X=\lceil \frac{e-s-1}{K-1} \rceil$번의 meeting만으로 문 $s+1, s+2, ..., e-1$을 통해 원하는 개수의 돌($p_i$개)이 지나도록 할 수 있음을 보이자. 0번 meeting을 위치 $s+1$에, 1번 meeting을 위치 $s+1+K-1$에, ..., $X-1$번 meeting을 위치 $s+1+(X-1)(K-1)$에서 진행하자. $l_i=s+1+i(K-1)$이라 하자. 그러면 $i$번 meeting은 $l_i, l_i+1, ..., l_{i+1}-1$번 문을 연다. $i$번 meeting이 진행될 때, $j\in [l_i, r_i]$에 대해 $j$번 문을 통해 $p_j$개의 돌이 지나가도록 할 것이다. 그러면 $i$번 meeting을 진행할 수 없다는 것은 $l_i$번 사람이 가지고 있는 돌의 수가 $p_{l_i}$보다 작거나, $l_{i+1}$번 사람이 가지고 있는 돌의 수가 $-p_{l_{i+1}-1}$보다 작음을 의미한다. 이제 $0, ..., X-1$번 meeting 중 최소 1개는 진행하는 것이 가능함을 보이자. 가능한 meeting이 없다고 가정하자. $0$번 meeting이 불가능하므로 $l_1$번 사람이 가지고 있는 돌의 수는 $-p_{l_1-1}$보다 작다. $p_{l_1-1}<0$이고 $1$번 meeting이 불가능하므로 $l_2$번 사람이 가지고 있는 돌의 수는 $-p_{l_2-1}$보다 작다. 이를 반복하면 $p_{l_{X-1}-1}<0$이라는 결론을 얻을 수 있다. 이는 $X-1$번 meeting이 가능하다는 것을 의미한다. 이는 가정에 모순이다. 따라서 $X$개의 meeting 중 가능한 것이 있다.
상수 $x$를 정한 뒤, $q_i=x$인 문 중 일부를 열지 말자. 문 $c_0, c_1, ..., c_Y$을 열지 않는다고 하자. 그러면 원은 $Y$개의 구간으로 나누어지고, 필요한 meeting의 수는 $\sum \lceil \frac{c_{i+1}-c_i-1}{K-1} \rceil$이다. 열지 않기로 했던 문을 열면, 두 구간이 합쳐지게 된다. $c_i$번 문을 열 경우, 필요한 meeting의 수가 어떻게 변화하는지 관찰하자. 편의상 $c_i-c_{i-1} \equiv 1 \textrm{ mod } K-1$이라면 $b_i=\textrm{true}$, $c_i-c_{i-1} \not\equiv 1 \textrm{ mod } K-1$이라면 $b_i=\textrm{false}$로 놓자. $(\textrm{not } b_i) \textrm{ and } (\textrm{not } b_{i+1})$인 경우에 $c_i$번 문을 열면 필요한 meeting의 수가 감소하거나 일정하다. $b_i$와 $b_{i+1}$ 중 하나만 만족하는 경우에는 meeting의 수가 일정하다. $b_i \textrm{ and } b_{i+1}$인 경우에는 meeting의 수가 증가한다. 따라서 최적해에서 문들을 적당히 더 열어서, $b_i$ 값들이 모두 true거나 하나만 false이도록 만들 수 있다.
문 $c_0, c_1, ..., c_Y$를 열지 않고, $c_{i+1} \equiv c_i+1\textrm{ mod } K-1$이라 하자. 이 때 필요한 meeting의 수는 $\lceil \frac{N-Y}{K-1} \rceil$이다. 따라서 이러한 $c_i$를 가능한 많이 고르자. 이는 $q_i=x$인 $i$를 모두 찾은 뒤, 그러한 $i$들을 $\textrm{mod }K-1$에 대해 분류하고, 이진탐색 등을 이용하여 구할 수 있다. $q_i=x$인 $i$의 개수를 $w$라 하면, $O(wlogw)$에 동작한다. 따라서 $O(NlogN)$에 문제를 해결할 수 있다.
H. Balanced Reversals
추가 예정.
'Codeforces' 카테고리의 다른 글
| Codeforces Round #594 (Div. 1) (0) | 2019.10.28 |
|---|---|
| Codeforces Round #591 (Div. 1) (0) | 2019.10.18 |
| Codeforces Round #588 (Div. 1) (0) | 2019.09.28 |