https://atcoder.jp/contests/agc039/tasks/agc039_a
https://img.atcoder.jp/agc039/editorial.pdf (Editorial)
대회는 시간이 안 맞아서 못 쳤고, 나중에 문제만 따로 풀었다. ABCDEF의 6문제가 출제되었고, 150분동안 A B C의 세 문제를 풀었다.
A. Connection and Disconnection
문자열 $S$가 주어진다. $S$를 $K$번 반복하여 문자열 $T$를 만든다. $T$의 특정 문자를 다른 문자로 바꾸는 연산을 할 수 있다. $T$에서 인접한 문자들이 서로 다르게 하려고 할 때, 필요한 연산 횟수의 최솟값은?
같은 문자가 반복해서 나오는 부분 문자열을 하나의 구간으로 생각하자. 길이 $x$의 구간에 대해 인접한 문자들이 서로 다르게 하기 위해서는 $\lfloor \frac{x}{2} \rfloor$번의 연산을 해야 한다. $S$가 몇 개의 구간으로 이루어져있고, 각 구간의 길이가 얼마인지 조사하자. 만약 구간이 1개라면, $S$는 하나의 문자로 이루어진 것이므로 $T$도 하나의 구간으로 이루어졌을 것이다. $S$의 가장 왼쪽 구간과 가장 오른쪽 구간이 같은 문자로 이루어졌다면, 이 두 구간은 $T$에서 합쳐질 것이다. 이 점을 고려하여 구현하면 선형 시간에 풀 수 있다.
B. Graph Partition
연결 그래프가 $G=(V, E)$가 주어진다. 정점들의 집합 $V$를 $V_1, V_2, ..., V_K$로 분할하고자 한다($V_1 \cup V_2 \cup ... \cup V_K=V, i\neq j \leftrightarrow V_i\cap V_j = \varnothing$). 이 때, 정점 $u\in V_i$와 $v\in V_j$를 잇는 간선이 존재한다면, $|i-j|=1$이어야 한다. 이러한 조건을 만족하는 분할이 존재하는지 확인하고, 존재한다면 가능한 $K$의 최댓값을 구하여라.
조건을 만족하는 분할이 존재한다면, 모든 간선은 번호의 기우성이 다른 두 집합에 있는 정점들을 이어야 한다. 따라서 그래프에 홀수 크기 사이클이 존재한다면 (=이분그래프가 아니라면) 이러한 분할은 존재하지 않는다. 이제 $K$의 최댓값을 구하자. 정점 $u\in V_i$와 정점 $v\in V_j$ 사이의 거리가 $dis$라면 $|i-j| \leq dis$이다. 따라서 그래프의 지름을 $d$라 하면, $K\leq d+1$가 성립한다. 그래프의 지름의 양 끝점을 $s, t$라 하자. $s$로부터의 거리가 $x$인 정점을 $V_{x+1}$에 넣으면 조건을 만족하는 분할이 되고, $K=d+1$이다. 따라서 그래프의 지름을 bfs를 이용하여 $O(N^2)$로 구하거나, Floyd-Warshall을 이용하여 $O(N^3)$에 구하면 된다.
*그래프의 지름 : $\textrm{max}\{\textrm{dis}(u, v) | u, v \in V \}$
C. Division by Two with Something
$N \in \mathbf{N}$과 이진수 $X < 2^N$이 주어진다. 어떤 이진수 $k$가 있을 때, 다음과 같은 연산을 한다. "$k$가 $2$로 나누어 떨어지면 $2$로 나눈 후 $2^{N-1}$을 더하고, 그렇지 않다면 $1$을 빼고 $2$로 나눈다." 이 연산을 몇 번을 반복해야 할 지 처음 수 $k$로 돌아올 지 알고 싶다. $0\leq k \leq X$에 대해, $k$로 돌아오기 위한 주기를 모두 더한 값을 구하여라. 돌아오지 않는다면 0을 더한다.
$k$의 모든 비트를 바꾼 후 $k$ 앞에 쓴다. 그러면 $2N$ 길이의 이진수가 생겼다. 이 이진수를 $Y$라 하자. 처음에는 $k$가 $Y$의 $[N, 2N)$부분이다. 연산을 할 때마다 $k$가 $[N-1, 2N-1), [N-2, 2N-2), ...$와 같이 변화한다. 주기적으로 반복하기 때문에 $[0, N)$ 다음에는 $2N-1$번째 수와 $[0, N-2)$로 구성되게 된다. 따라서 연산을 $2N$번 시행하면 무조건 $k$로 돌아오며, 최소 주기는 $2N$의 약수라는 것을 알 수 있다. 이제 이 최소 주기를 구해보자. 최소 주기가 $T$라 하자($T|2N$). $Y$의 $[N-T, 2N-T)$와 $[N, 2N)$이 일치한다. $T$가 $N$의 약수라면, $[N-T, N), [N, N+T), ..., [2N-T, 2N)$이 일치하게 된다. 그러나 $[N-T, N)$은 $[2N-T, 2N)$의 비트를 뒤집은 것이므로 같을 수 없다. 따라서 $T$는 $N$의 약수가 아니다. $N=2^KM$이라 하자($M$은 홀수). 그러면 $T=2^{K+1}S$가 된다($S$는 홀수). 이를 이용하면 $Y$의 $[N, N+\frac{T}{2}), [N+T, N+\frac{3}{2}T), ..., [2N-\frac{T}{2}, 2N)$이 일치하고, $[N+\frac{T}{2}, N+T), [N+\frac{3}{2}T, N+2T), ..., [2N-T, 2N-\frac{T}{2})$이 $[N, N+\frac{T}{2})$의 비트를 뒤집은 것과 일치한다는 사실을 알 수 있다. $X$의 앞 $\frac{T}{2}$ 자리를 $X'$이라고 했을 때, 주기가 $T$인 수는 $X'$ 또는 $X'+1$개가 있다. 이는 $O(N)$에 확인할 수 있다. 여기서 주기가 $T$보다 작은 $T$의 약수인 경우를 빼주면 된다. 약수의 개수를 $d$라 하면, 답을 $O(Nd)$에 구할 수 있다. $d \leq 2\sqrt{N}$이므로 시간 안에 동작한다는 것을 알 수 있다. 실제로는 $d \leq 72$이다.
D. Incenters
단위원 위에 $N$개의 서로 다른 점이 주어진다. 이 점들 중 임의로 3개를 골라서 삼각형을 만든다. 이 삼각형의 내심의 좌표의 기댓값은?
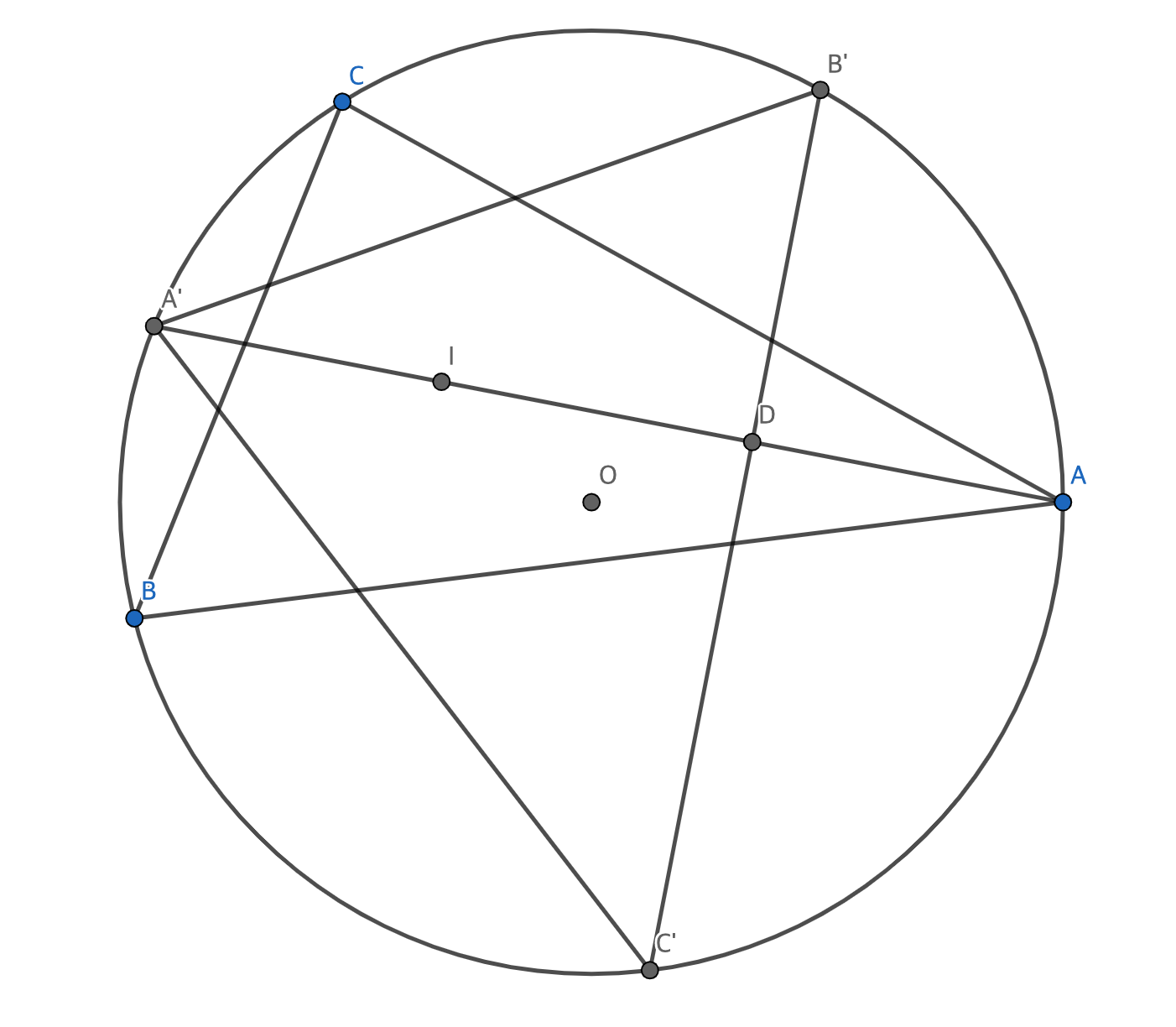
세 점을 $\rm A, B, C$라 하자. 점 $\rm A$를 포함하지 않는 $\overset{\frown}{\rm BC}$의 중점을 $\rm A'$이라 하자. 점 $\rm B', C'$도 마찬가지로 정의하자. 그러면 $\triangle \rm ABC$의 내심과 $\triangle \rm A'B'C'$의 수심은 일치한다.
pf) $\rm A'$은 $\overset{\frown}{\rm BC}$의 중점이므로 $\angle \rm A'IB=\angle \rm A'IC$이고, 따라서 $\angle \rm A'AB = \angle \rm A'AC$이다. 점 $\rm A'$이 $\angle \rm BAC$의 이등분선 위의 점이므로 $\triangle \rm ABC$의 내심 $\rm I$는 $\overline{\rm AA'}$ 위의 점이다. $\overline{\rm AA'}$과 $\overline{\rm B'C'}$의 교점을 $\rm D$라 하자. $\angle \rm A'D'B'=180˚-\angle AA'B' - \angle A'BC' \\= 180˚-\frac{1}{2}\angle AOB' - \frac{1}{2}\angle A'OC'\\= 180˚-\frac{1}{2}\angle AOB' - \frac{1}{2}\angle A'OB - \frac{1}{2}\angle BOC'\\= 180˚-\frac{1}{4}\angle AOC - \frac{1}{4}\angle COB - \frac{1}{4}\angle BOA \\= 90˚$
$\rm B', C'$에 대해서도 마찬가지이므로 점 $I$는 $\triangle \rm A'B'C'$의 수심이다.
삼각형에서 수심($\rm H$), 무게중심($\rm G$), 외심($\rm O$)는 한 직선 상에 있으며, $\overline{\rm HG}:\overline{\rm GO} = 1:2$이라는 성질이 있다. $\triangle \rm A'B'C'$의 외심은 원점이므로 무게중심의 기댓값을 구하면 된다. 무게중심의 좌표는 세 꼭짓점의 좌표의 평균이므로 구하기 쉽다. 점 $B, C$가 정해지면 $A'$도 정해진다. 점 $A$의 위치 또한 정해야 하므로 $\overset{\frown}{\rm BC}$위에 있는 점들의 개수를 고려하여 계산하면 된다. 따라서 문제를 $O(N^2)$에 해결할 수 있다.
E. Pairing Points
추가 예정.
F. Min Product Sum
추가 예정.